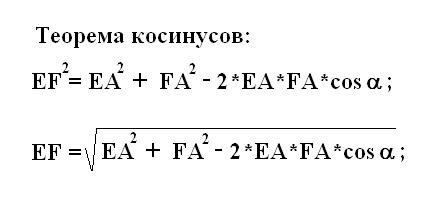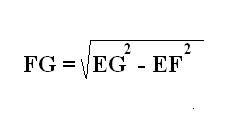Протестант

Все про все

периметр трикутника

Рада 1: Як виявити боку, якщо вести периметр

Периметром плоскої фігури називають суму довжин усіх її сторін. Але виявити боку фігури, знаючи тільки периметр – не незмінне здійсненне завдання. Найчастіше потрібні додаткові дані.

Інструкція

1. Для квадрата або ромба завдання виявити боку з периметра вирішується дюже примітивно. Звісно, ​​що у цих 2-х фігур по 4 сторони і всі вони рівні між собою, слідчо периметр p квадрата і ромба дорівнює 4a, де a – сторона квадрата або ромба. Тоді довжина сторони дорівнює одній четвертій периметра: a = p / 4.
2. Легко можна вирішити це завдання і для рівностороннього трикутника. У нього три ідентичних по довжині боку, слідчо периметр p рівностороннього трикутника дорівнює 3a. Тоді сторона рівностороннього трикутника a = p / 3.
3. Для інших фігур потрібні додаткові дані. Скажімо, можна виявити сторони прямокутника, знаючи його периметр і площу. Уявімо, що довжина 2-х протилежних сторін прямокутника дорівнює a, а довжина 2-х інших сторін – b. Тоді периметр p прямокутника дорівнює 2 (a + b), а площа s дорівнює ab. Отримаємо систему рівнянь з двома невідомими: p = 2 (a + b) s = ab.Виразім з першого рівняння а: а = p / 2 – b. Підставимо в друге рівняння і знайдемо b: s = pb / 2 – b². Дискримінант цього рівняння D = p² / 4 – 4s. Тоді b = (p / 2 ± D ^ 1/2) / 2. Відкиньте той корінь, той, що буде трохи менше нуля, і підставте в вираз для сторони a.

Рада 3: Як виявити сторони прямокутника

Окремий випадок паралелограма – прямокутник – знаменитий тільки в геометрії Евкліда. У прямокутника рівні всі кути, і кожен із них окремо становить 90 градусів. Виходячи з приватних властивостей прямокутника, а також з властивостей паралелограма про паралельність протилежних сторін дозволено виявити боку фігури за заданим діагоналям і розі від їх перетину. Обчислення сторін прямокутника базується на додаткових побудовах і використанні властивостей одержуваних фігур.

1. Побудуйте прямокутник EFGH. Запишіть знамениті дані: діагональ прямокутника EG і кут α, отриманий від перетину 2-х рівних діагоналей FH і EG. Побудуйте на малюнку діагоналі і зауважте між ними кут α.

2. Буквою А зауважте точку перетину діагоналей. Роздивіться утворений побудовами трикутник EFА. Відповідно до властивості прямокутника його діагоналі рівні і діляться навпіл точкою перетину А. Обчисліть значення FА і EА. Тому що трикутник EFА є рівнобедреним і його боку EА і FА рівні між собою і відповідно рівні половині діагоналі EG.
3. Далі обчисліть першу сторону EF прямокутника. Дана сторона є третьою невідомою стороною розглянутого трикутника EFА. Згідно з теоремою косинусів за відповідною формулою виявіть сторону EF. Для цього підставте в формулу косинусів отримані раніше значення сторін FА дорівнює EА і косинус знаменитого кута між ними α. Обчисліть і запишіть отримане значення EF.

4. Виявіть другу сторону прямокутника FG. Для цього роздивіться інший трикутник EFG. Він є прямокутним, де знамениті гіпотенуза EG і катет EF. Згідно з теоремою Піфагора виявіть 2-й катет FG за відповідною формулою.

5. У відповідності з властивостями прямокутника його протилежні ребра рівні. Таким чином сторона GH дорівнює виявленої стороні EF, а HЕ = FG. Запишіть в результат все обчислені сторони прямокутника.

Рада 4: Як виявити периметр рівностороннього трикутника

Рівносторонній трикутник нарівні з квадратом є, ймовірно, найбільш примітивний і симетричною фігурою в планіметрії. Зрозуміло, все співвідношення, об'єктивні для звичайного трикутника, правильні також і для рівностороннього.Втім для позитивного трикутника все формули стають набагато простіше.

Вам знадобиться

1. Щоб виявити периметр рівностороннього трикутника виміряйте довжину однієї з його сторін і помножте результат вимірювання на три. У вигляді формули це правило дозволено записати подальшим чином: Прт = Дс * 3, де: Прт – периметр рівностороннього трикутника, Дс – довжина всякий з його сторон.Періметр трикутника вийде в тих же одиницях виміру, що і довжина його боку.
2. Прімер.Дліна боку рівностороннього трикутника дорівнює 10 мм. Потрібно визначити його періметр.Решеніе.Прт = 10 * 3 = 30 (мм)
3. Тому що рівносторонній трикутник володіє високим ступенем симетрії, то для обчислення його периметра досить одного з параметрів. Скажімо, площі, висоти, радіуса вписаного або описаного кола.
4. Якщо вести радіус вписаного кола рівностороннього трикутника, то для обчислення його периметра скористайтеся подальшої формулою: Прт = 6 *? 3 * r, де: r – радіус вписаного окружності.Ето правило випливає з того, що радіус вписаного кола рівностороннього трикутника виражається через довжину його сторони подальшим співвідношенням: r =? 3/6 * Дс.
5. Щоб обчислити периметр позитивного трикутника через радіус описаного кола, застосуйте формулу: Прт = 3 *? 3 * R, де: R – радіус описаної окружності.Данная формула легко виводиться з того факту, що радіус описаного кола вірного трикутника виражається через довжину його боку подальшим співвідношенням: R =? 3/3 * Дс.
6. Для обчислення периметра рівностороннього трикутника через звісно площа скористайтеся подальшим співвідношенням: Sрт = Дст? *? 3/4, де: Sрт – площа рівностороннього треугольніка.Отсель дозволено вивести: ДСТ? = 4 * Sрт /? 3, слідчо: ДСТ = 2 *? (Sрт /? 3) .Подставляя це співвідношення в формулу периметра через довжину сторони рівностороннього трикутника, отримуємо: Прт = 3 * ДСТ = 3 * 2 *? (Sрт / ? 3) = 6 *? Sст /? (? 3) = 6? Sст / 3 ^ ?.
Відео по темі

Рада 5: Як виявити площа і периметр квадрата

Квадрат є геометричну фігуру, що складається з чотирьох сторін ідентичною довжини і чотирьох прямих кутів, кожен із яких дорівнює 90 °. Визначення площі або периметра чотирикутника, причому будь-якого, потрібно не тільки при вирішенні завдань з геометрії, але і в повсякденному житті. Ці знання можуть стати придатними, скажімо, під час ремонту при розрахунку необхідного числа матеріалів – покриттів для підлоги, стін або стелі, а також для розбивки газонів і грядок і т.д.

1. Для визначення площі квадрата помножте величину довжини на величину ширини. Тому що в квадраті довжина і ширина ідентичні, то значення одного боку досить побудувати в квадрат. Таким чином, площа квадрата дорівнює довжині його боку, яка була зведена в квадрат. Одиницею вимірювання площі можуть бути квадратні міліметри, сантиметри, дециметр, метри, кілометри.Даби визначити площу квадрата, дозволено скористатися формулойS = aa, де S – площа квадрата, а – сторона квадрата.
2. Приклад № 1. Кімната має форму квадрата. Скільки ламінату (в кв.м) знадобиться для того, щоб повністю покрити підлогу, якщо довжина одного боку кімнати становить 5 метров.Запішіте формулу: S = aa. Підставте в неї зазначені в умові данние.Потому що а = 5 м, слідчо, площа буде равнаS (кімнати) = 5х5 = 25 кв.м, значить, і S (ламінату) = 25 кв.м.
3. Периметр є загальну довжину кордону фігури. В квадраті периметр – це довжина всіх чотирьох, причому ідентичних, сторін. Тобто, периметр квадрата є сумою всіх його чотирьох сторін. Щоб обчислити периметр квадрата, досить знати довжину однієї його сторони. Вимірюється периметр в міліметрах, сантиметрах, дециметрах, метрах, кілометрах.Для визначення периметра є формула: P = a + а + а + а іліP = 4a, гдеР – периметр, а – довжина сторони.
4. Приклад № 2.Для оздоблювальних робіт приміщення в формі квадрата потрібні стельові плінтуса. Обчисліть загальну довжину (периметр) плінтусів, якщо величина одного боку кімнати дорівнює 6 метрів. Запишіть формулу P = 4a.Подставьте в неї зазначені в умові дані: Р (кімнати) = 4 х 6 = 24 метра.Следственно, довжина стельових плінтусів теж буде дорівнює 24 метрів.
Відео по темі

Периметром трикутника, як в іншому і будь-якої фігури, називається сума довжин всіх сторін. Досить часто це значення допомагає знайти площу або використовується для розрахунку інших параметрів фігури.

Формула периметра трикутника виглядає так:

Формула розрахунку периметра рівнобедреного трикутника буде виглядати так:

Формула розрахунку периметра рівностороннього трикутника:

Загалом, коли всі сторони дані, знайти периметр досить просто. В інших же ситуаціях потрібно знайти розмір якої бракує боку. У прямокутному трикутнику можна знайти третю сторону по теоремі Піфагора.

Трикутник, у якого є кут 90 °

Його називають прямокутним. Наявність прямого кута дає можливість знаходити невідомі сторони, користуючись визначенням тригонометричних функцій і теоремою Піфагора. Найдовша сторона називається гіпотенуза і позначається c. Є ще дві сторони, a і b. Дотримуючись теоремі, що носить ім'я Піфагора, маємо c2 = a2 + b2. Катети a = √ (c2 – b2) і b = √ (c2 – А2). Знаючи довжину двох катетів a і b, обчислюємо гіпотенузи. Потім знаходимо суму сторін фігури, склавши ці значення. Завдання: Катети прямокутного трикутника мають довжину 8,3 сантиметра і 6,2 сантиметра. Периметр трикутника потрібно обчислити. Вирішуємо: Позначимо катети a = 8,3 см, b = 6,2 см. За теоремою Піфагора гіпотенуза c = √ (8,32 + 6,22) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Або P = 8,3 + 6,2 + √ (8,32 + 6,22) = 24,9 (см). Відповідь: P = 24,9 см. Значення коренів брали з точністю до десятих. Якщо нам відомі значення гіпотенузи і катета, то значення Р отримаємо, обчисливши Р = √ (c2 – b2) + b + c. Завдання 2: Відрізок земельної ділянки, що лежить проти кута в 90 градусів, 12 км, один з катетів – 8 км. За який час можна обійти всю ділянку, якщо рухатися зі швидкістю 4 кілометри на годину? Рішення: якщо найбільший відрізок – 12 км, менший b = 8 км, то довжина всього шляху складе P = 8 + 12 + √ (122 – 82) = 20 + √80 = 20 + 8,9 = 28,9 (км) . Час знайдемо, розділивши шлях на швидкість. 28,9: 4 = 7,225 (ч). Відповідь: можна обійти за 7,3 год. Значення квадратних коренів і відповіді беремо з точністю до десятих. Можна знайти суму сторін прямокутного трикутника, якщо дана одна зі сторін і значення одного з гострих кутів. Знаючи довжину катета b і значення протилежного йому кута β, знайдемо невідому сторону a = b / tg β. Знаходимо гіпотенузу c = a: sinα. Периметр такої фігури знаходимо, склавши отримані значення. P = a + a / sinα + a / tg α, або P = a (1 / sin α + 1 + 1 / tg α). Завдання: У прямокутному Δ АВС з прямим кутом С катет ВС має довжину 10 м, кут А – 29 градусів. Потрібно знайти суму сторін Δ АВС. Рішення: Позначимо відомий катет ВС = a = 10 м, кут, що лежить навпроти нього, ∟А = α = 30 °, тоді катет АС = b = 10: 0,58 = 17,2 (м), гіпотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Або Р = 10 · (1 + 1,72 + 2) = 47,2 м. Маємо: P = 47,2 м. Значення тригонометричних функцій беремо з точністю до сотих, значення довжини сторін і периметра округляємо до десятих. Маючи значення катета α і прилеглого кута β, дізнаємося, чому дорівнює другий катет: b = a tg β. Гіпотенуза в такому випадку буде дорівнює катету, розділеному на косинус кута β. Периметр дізнаємося за формулою P = a + a tg β + a: cos β = (tg β + 1 + 1: cos β) · a. Завдання: Катет трикутника з кутом 90 градусів 18 см, прилегла кут – 40 градусів. Знайти P. Рішення: Позначимо відомий катет ВС = 18 см, ∟β = 40 °. Тоді невідомий катет АС = b = 18 · 0,83 = 14,9 (см), гіпотенуза АВ = c = 18: 0,77 = 23,4 (см). Сума сторін фігури дорівнює Р = 56,3 (см). Або Р = (1 + 1,3 + 0,83) * 18 = 56,3 см. Відповідь: P = 56,3 см. Якщо відома довжина гіпотенузи c і який-небудь кут α, то катети будуть рівні твору гіпотенузи для першого – на синус і для другого – на косинус цього кута. Периметр цієї фігури P = (sin α + 1+ cos α) * c. Завдання: Гіпотенуза прямокутного трикутника АВ = 9,1 сантиметр, а кут 50 градусів. Знайти суму сторін даної фігури. Рішення: Позначимо гіпотенузу: AB = c = 9,1 см, ∟A = α = 50 °, тоді один з катетів BC має довжину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9 , 1 · 0,64 = 5,8 (см). Значить периметр цього багатокутника дорівнює P = 9,1 + 7 + 5,8 = 21,9 (см). Або P = 9,1 · (1 + 0,77 + 0,64) = 21,9 (см).Відповідь: P = 21,9 сантиметрів.

Сума сторін довільного трикутника, у якого довжини двох сторін невідомі

Коли знаємо довжину тільки одного відрізка і значення двох кутів, можна дізнатися довжину двох невідомих сторін, користуючись теоремою синусів: «в трикутнику сторони завжди пропорційні значенням синусів протилежних кутів». Звідки b = (a * sin β) / sin a. Аналогічно c = (a sin γ): sin a. Периметр в такому випадку буде P = а + (а sin β) / sin a + (a sin γ) / sin a. Завдання: Маємо Δ ABC. У ньому довжина сторони BC 8,5 мм, значення кута C – 47 °, а кута B – 35 градусів. Знайти суму сторін даної фігури. Рішення: Позначимо довжини сторін BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α = 47 °, ∟B = β = 35 °, ∟ C = γ = 180 ° – (47 ° + 35 °) = 180 ° – 82 ° = 98 °. Зі співвідношень, отриманих з теореми синусів, знаходимо катети AC = b = (8,5 · 0,57): 0,73 = 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм). Звідси сума сторін цього багатокутника дорівнює P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Відповідь: P = 23,5 мм. У разі, коли є тільки довжина одного відрізка і значення двох прилеглих кутів, спочатку обчислюємо кут, протилежний відомої стороні. Всі кути цієї фігури в сумі мають 180 градусів. Тому ∟A = 180 ° – (∟B + ∟C). Далі знаходимо невідомі відрізки, використовуючи теорему синусів. Завдання: Маємо Δ ABC. Він має відрізок BC, рівний 10 см. Значення кута B дорівнює 48 градусів, кут C дорівнює 56 градусів. Знайти суму сторін Δ ABC. Рішення: Спочатку знайдемо значення кута A, протилежного стороні BC. ∟A = 180 ° – (48 ° + 56 °) = 76 °. Тепер з теоремою синусів обчислимо довжину сторони AC = 10 · 0,74: 0,97 = 7,6 (см). AB = BC * sin C / sin A = 8,6. Периметр трикутника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.

Читайте також:

Площа рівностороннього трикутника через сторонуОнлайн-калькулятор для розрахунку площі трикутника допоможе Вам знайти площу трикутника декількома …

Що таке периметр і як його знайти? Геометрія, якщо не помиляюся, в мій час вивчалася з …

Завдання №1Условіе. Площа прямокутної трапеції відома і дорівнює 120 дм2. Її висота має довжину 8 …